Skip to content

What is a Circle Times a Circle?

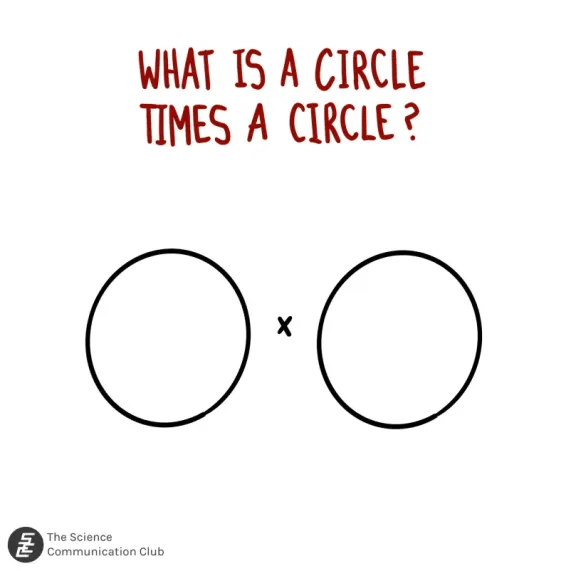
Two circles with the multiplication sign between them with the title reading “What is a circle times a circle?”

Written by Rishibh Prakash
Illustrated by Rebecca Parvaneh

It may seem like a nonsense question, but we can actually give a pretty meaningful answer. Let’s start by considering the simpler case: what is a line times a line? When multiplying numbers, say “three times five”, we mean we have “three lots of five” or for every point in a group of three, we have a group of five. Similarly then, a line times a line should mean that for every point on a line, we have another line. In other words, we get a square! (Or if you prefer your lines to be infinite, we get a plane).

Two lines with the multiplication sign between them in an equation-like format followed by the equals sign showcasing a main line with other lines pointing downward connected to each point on the main line. The title reads “What is a line times a line?”

Let’s keep playing with this to see where it takes us. For example, what is the product of a circle and a line? Well to every point on the circle, we attach a line and so we get a cylinder! Now to get back to the titular question, what is a circle times a circle? We have a circle and to every point we need to attach a circle. This is maybe slightly trickier to visualize but if you play around with it in your head you should be able to convince yourself that the answer is a donut¹!

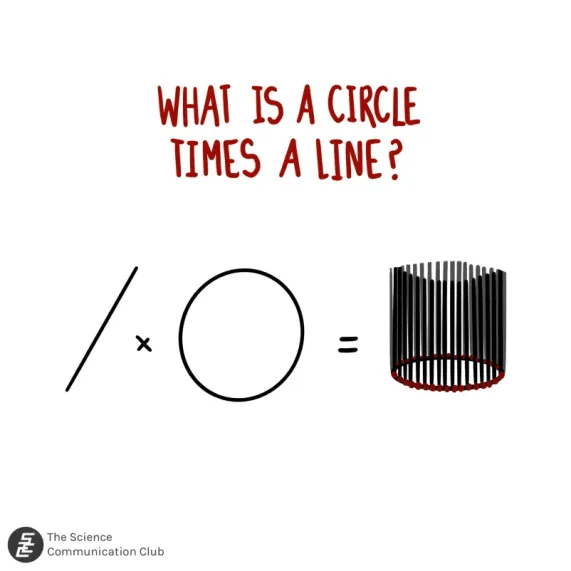
A line followed by a multiplication sign and a circle followed by an equals sign showcasing a cylinder where every point on the circle (bottom face) is attached to a line pointing straight up. The title reads “What is a circle times a line?”
Two circles with the multiplication sign between them in an equation-like format followed by an equals sign showcasing a torus (a circle with other circles attached to each point on the main circle). The title reads “What is a circle times a circle?”

Now, we could keep playing with this, asking how we can combine these and other shapes and what the result would be (for instance, what would a circle times a circle times a line be?). But there is an adjacent question that may have popped in your head as we’re doing this. We concluded that a cylinder is simply a circle with a line attached to every point on the circle. But is that a complete description of a cylinder? In other words, could you have a shape which is a circle with a line attached to every point but is not a cylinder? In fact, the answer is yes!

We can come up with such a shape without too much difficulty. One way to form a cylinder is to take a rectangular piece of paper and glue a pair of opposite sides together. Now imagine you do this but before gluing the sides together, you perform a half-twist. This gives you something called the Möbius strip. In the middle of it, you will see a circle and at every point in this circle, we have a line!

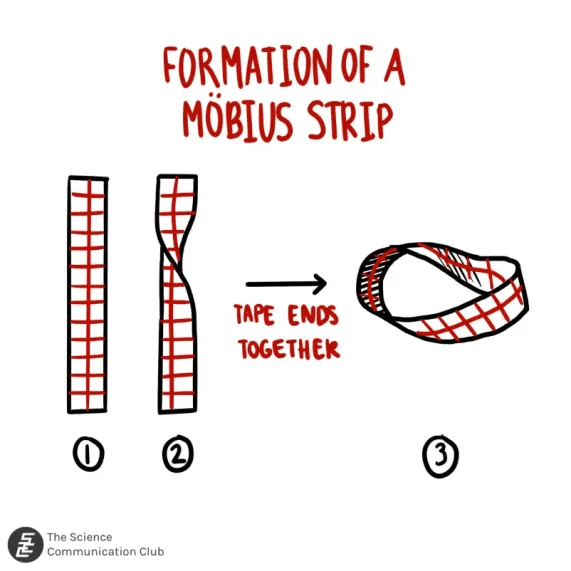
A rectangular piece of paper laid down flat followed by the same rectangular piece of paper with a slight twist applied to it. After attaching the short ends of the rectangular piece of paper together a Möbius is obtained. The title reads “Formation of a Möbius strip”.

The Möbius strip has lots of interesting properties. For one thing it has only one side! Start at some place in the middle and follow the central circle (sometimes called the core circle) around. You will notice that by the time you come back you are actually on the opposite side of the paper! You have to go around again to come back exactly where you started. Compare this with the cylinder where there is no way to go from the ‘outside’ to the ‘inside’ without crossing the boundary (in this way we think of the cylinder as having two sides).

Now, my dear reader, I imagine there is a question burning in your head. Can we do the same thing with the donut? Can we find another shape that has a circle attached to every point on a circle but is not a donut? Indeed, we can. I will encourage you to try to come up with an answer yourself although I will also warn you that the answer is not so easy.

In fact, a completely analogous trick to the Möbius strip works. There we took a cylinder, cut it to get a rectangle, flipped one of the edges and then glued it back to get the strip. In this case, we can do almost exactly the same thing: we take a torus, cut it to get a cylinder, flip one of the boundary circles (this is the tricky part) and then glue things back together again.

Starting out with a square piece of material and attaching two sides together, a cylinder is formed. More structures are added to the shape until the shape funnels into itself creating a Klein Bottle. The title reads “Formation of a Klein Bottle”.

You might argue that this looks nothing like a circle times a circle, and in particular you may be pointing at the self-intersecting portion of the surface. This is a problem not of our construction but of dimensions. If we had four dimensions to work in we could create this surface very nicely without this intersection. Consider how, when drawn in 2D, the Möbius strip also looks like its intersecting itself. It’s only when we realise it in three dimensions, do we see that this is not really the case. Completely analogously, the Klein bottle only looks like it’s intersecting itself when ‘drawn’ in 3D. Were we to view it in its full glory in four dimensions, this would not be so.

This is one of the delightful aspects of mathematics. Even simple questions about donuts can lead us to (literally) unimaginable places, all from the comfort of our desks.

Footnotes:

  1. To be precise, it’s just the surface of the donut, or the torus, as it’s known mathematically.

Tags: