Written by Rishibh Prakash
Illustrated by Irene Ma
Maths in school, and even university to some extent, always seems to have so many rules. For many people, acing maths classes simply amounted to memorising all the rules. Know your trig identities, the chain rule, the power rule, know the integrals of all your functions and you would be golden. But let me tell you a secret: the rules are all made up. Numbers and functions are just abstract ideas. They are not bound by any rules or laws, not even the laws of physics. In some sense, that’s what makes them so powerful. However, this also means they are powerless to our whimsy. We can set the rules to be what we want. In order to demonstrate this, let’s see what happens if you break the most fundamental of rules: let’s say 0 = 1.
What happens to all the other numbers in this case? Well, let’s see: 2 = 1 + 1 and if 1 = 0, we have 1 + 1 = 0 + 0 = 0. So, 2 = 0. Similarly, we conclude that 3 = 0 and 4 = 0 and so on. And of course, we can go the other way as well. -1 = -1 + 0 = -1 + 1 = 0. Hence, we conclude that if 0 = 1, then all the integers must be 0. Then is everything 0? Let’s look at 1.5 = 1 + 0.5. But since 1 = 0, we get 1 + 0.5 = 0 + 0.5, which means 1.5 = 0.5. Repeating these arguments, what we get is … -2.5 = -1.5 = -0.5 = 0.5 = 1.5 = 2.5 = …. Replacing 0.5 with any other number between 0 and 1 gives us very similar results. For example, 4.321 = 0.321. So asserting 0 = 1 means that we end up forgetting about the whole-number part of a number and only caring about the decimal part.

If you’re confused, here’s a (hopefully) helpful analogy. Consider Pythagoras’ greedy cup (see figure below). It is a cup that works just like any other cup except for the fact that if you fill it to the very top, it empties itself (the idea being to stop people from getting greedy and taking large quantities of wine for themselves). In this case then, having one full cup is really the same as having an empty cup because the cup empties itself as soon as it’s full. You can imagine a similar thing going on with our numbers: we start from 0 and keep increasing until we hit 1, at which point we “overflow” and return back to 0.
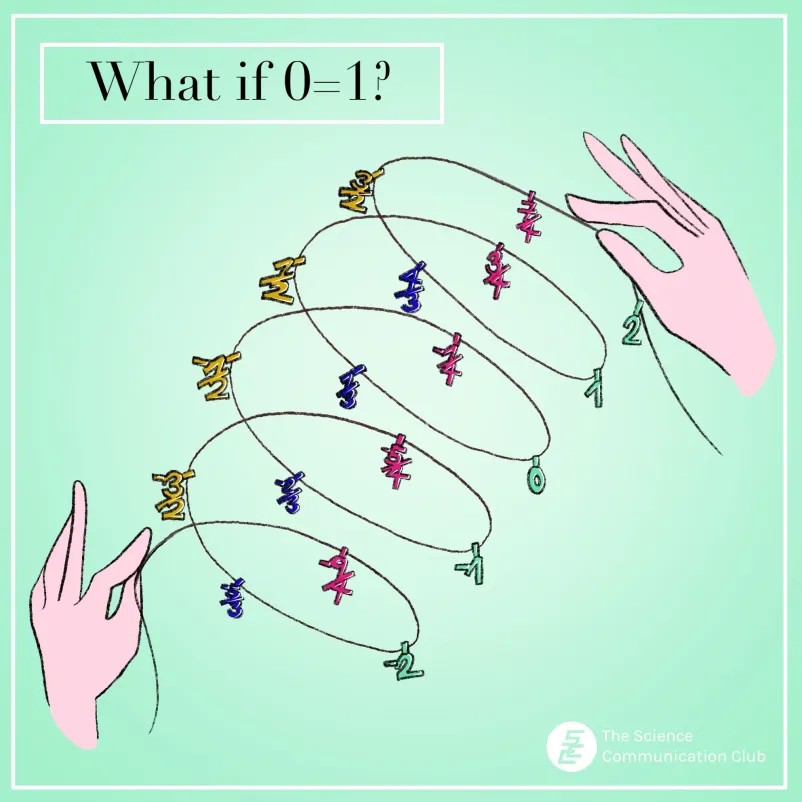
You could stop here and consider this just a fun tidbit. But let’s take this seriously and ask: what do numbers in this setting actually look like and behave? The numbers we are used to working with lie on a number line which extends infinitely far in both directions. What happens to this line when we assert 0 = 1?
Suppose you travel on the usual number line from 0 to 2. In the new system, the path from 0 to 1 looks the exact same as the path from 1 to 2 (remember, we’re only looking at the decimal parts!). So somehow going from 0 to 1, you end up back where you started which allows you to go over the same path twice. In other words, what we have now is a circle!

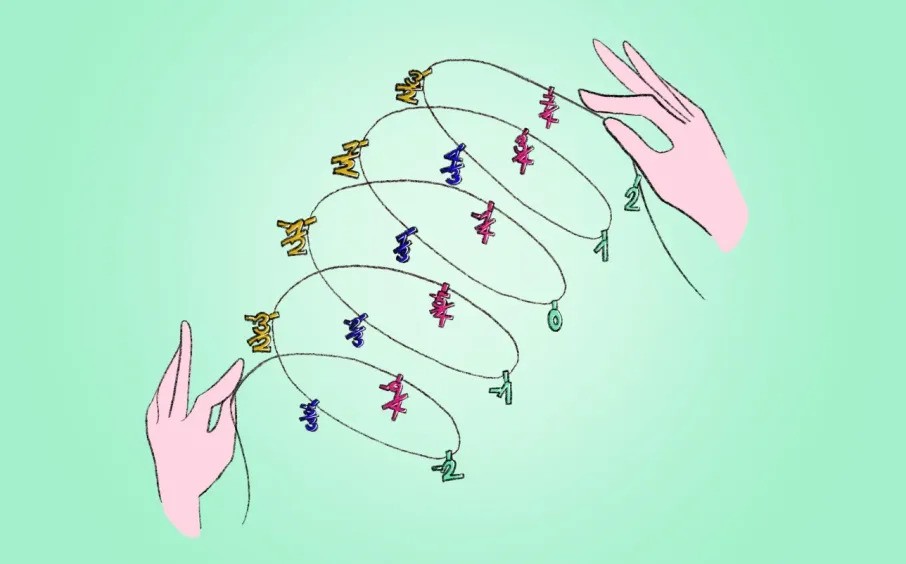

And of course, we’ve only just begun to scratch the surface here. So far, we’ve only talked about addition. What about multiplication? (You have to be slightly careful, but you can make it work.) For the particularly adventurous, we can even start thinking about functions and calculus with these numbers (yes, you can make it all work!).
To recap, all we did was define some new rule and see what its consequences are. More than functions and numbers and calculus, this is what mathematics is all about. It’s all about studying the patterns and structures that naturally emerge from our rules. So go and mess around with the rules of this game and see where it lands you. You might be surprised by where it takes you (or maybe you end up where you started, just going in a circle!).
Sources:
Wikipedia contributors. Pythagorean cup [image]. Wikipedia, The Free Encyclopedia; 2016 Jul 8, 13:45 UTC [accessed 2024 Oct 10]. https://en.wikipedia.org/wiki/File:Physagorian_Pythagoras_Greedy_Tantalus_cup_05.svg