The Axiom of Choice in Action

Let us assume AC and solve a nice puzzle using it.

The Prisoners’ Hat Puzzle

“A countably infinite number of prisoners, each with an unknown and randomly assigned red or blue hat line up in a single file line. Each prisoner faces away from the beginning of the line, and each prisoner can see all the hats in front of him and none of the hats behind. Starting from the beginning of the line, each prisoner must correctly identify the color of his hat, or he is killed on the spot. The prisoners have a chance to meet beforehand, but once in line, no prisoner can hear what the other prisoners say. Is there a way to ensure that only finitely many prisoners are killed?” ³

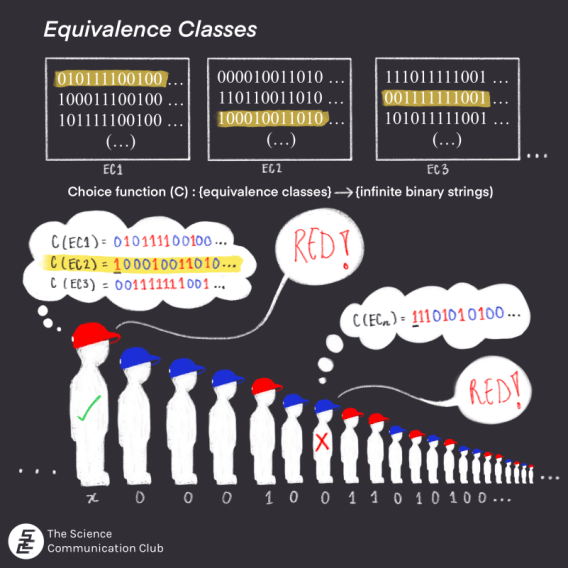
Yes, there is! Here’s what the prisoners need to do. First, they label blue hats with a 0 and red hats with 1. For example, if the first person has a blue hat and the second person has a red hat, then the code for the line of prisoners’ hats looks like (01…) So, all possible combinations of hats is the set of all infinite binary strings.

            Next, form a “rule” on this set by asserting that any two infinite binary strings, for example (a₁ a₂ a₃ …) and (b₁ b₂ b₃ …), are equivalent to each other if they differ on only finitely many indices. For example, the string consisting of alternating 0s and 1s (10101010101010101010…) is equivalent to the string (1111101010101010…) because both strings’ numbers match after the 4th index. Using this equivalence relation, the prisoners sort the set of all possible infinite binary strings into groups of “equivalence classes”, where two binary strings are in the same group if they are equivalent to each other. Then, prisoners pick one representative binary string from each of these equivalence classes. To pick one binary string from each equivalence class, the prisoners need a choice function on the set of equivalence classes. AC guarantees that there exists at least one choice function on this set, so prisoners can use that choice function to decide which binary string to pick from each equivalence class.

Finally, when prisoners are put into the file line, all they need to do is look at the hats in front of them, identify that pattern with a string, figure out which equivalence class this string is in, and remember the representative binary string that they picked for that equivalence class using the choice function. Then, the nᵗʰ person in the line will say the nᵗʰ element of this representative string. Since the actual string (the one that is formed by looking at the hats) is equivalent to this representative string, they differ at only finitely many indices, and therefore only finitely many prisoners will say the wrong colour and be killed.